y = xtan (ln x C) This is a first order linear homogeneous equation NB here homogeneous has its own meaning it means that the equation can be written in form y' = f(x,y) and that f(kx, ky) = f(x,y) for constant k so standard approach is to let v = y/x so y = v * x y' = v' x v thus, plugging this into the original v' x v = v^2 v 1 v' x = v^2 1 (v')/(v^2 1) = 1/(v^2 1To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2)dy/dx2xy=(x^22)(x^21)`Question dy = x2 (Sin2x 2xy) dx y(1) = 2 calculate the values of y(x) when 1

For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube
If dy/dx=x^2+y^2+1/2xy
If dy/dx=x^2+y^2+1/2xy-Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to How do you use Implicit differentiation find #x^2 2xy y^2 x=2# and to find an equation of the tangent line to the curve, at the point (1,2)?




Solve The Following X Dy Dx Y X 2 Dy Dx 2y Chegg Com
May be substituchion z = x2 − y2 xy2 or we can be it more simple To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `dy/dx=(x^23y^2)/(2xy)`Exercise 1 1 x dy − y x2 dx = 0 Exercise 2 2xy dy dx y2 −2x = 0 Exercise 3 2(y 1)exdx2(ex −2y)dy = 0 Theory Answers Integrals Tips Toc JJ II J I Back Section 2 Exercises 5 Exercise 4 (2xy 6x)dx(x2 4y3)dy = 0 Exercise 5 (8y −x2y) dy dx x−xy2 = 0 Exercise 6
1 1 y dy dx = x2 ∫ 1 1 y dy dx dx = ∫ x2 dx ∫ 1 1 y dy = ∫ x2 dx ln(1 y) = x3 3 C 1 y = ex3 3 C = ex3 3 eC = Cex3 3 y = Cex3 3 −1 Applying the IV 3 = Ce0 −1 = C −1 ⇒ C = 4 y = 4ex3 3 −1Then y ′ (x) = − w (x) 2 1 ⋅ w ′ (x), so the differential equation becomes w (x) 2 (1 x) 2 w ′ (x) x w (x) x 2 = 0, that is w ′ (x) (1 x) 2 x w (x) (1 x) 2 x 2 = 0 Solve (1x^2)dy/dx 2xy = x(1x^2)^{1/2} Solve the differential equation (x^2 y^2)dy/dx = 2xy given that y = 1, x = 1 asked in Differential equations by AmanYadav ( 556k points) differential equations
Solution for 24 Solve the following DE x² dy 2xy ln y (x²y–y)ln³y =0 dxFor the differential equation `(x^2y^2)dx2xy dy=0`, which of the following are true (A) solution is `x^2y^2=cx` (B) `x^2y^2=cx` `x^2y^2=xc` (D) `y Solve differential equations (x 2y 2 − 1)dy 2xy 3dx = 0 We now what ∂M ∂y = 2x2y and ∂N ∂x = 2y3 I try to make it exact but get this x2 − y2 xy2 Help me!
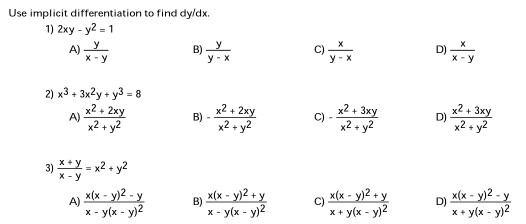



Use Implicit Differentiation To Find Dy Dx 1 2xy Y2 Chegg Com




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When
Use separation of variables math\dfrac{dy}{dx}=2xy/math math\implies\dfrac{1}{y}\left(\dfrac{dy}{dx}\rightSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreHow do I solve the differential equation dy/dx=2xy?




Solving Differential Equation 2xy Dy Dx Y 2 X 2 0 Youtube




Solve This Differential Equation Dy Dx 1 2xy X 2 Chegg Com
`2xy (dy)/(dx) = x^(2) 3y^(2)`Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThe solution of differential equation (x 2 y – 2xy 2) dx – (x 3 – 3x 2 y) dy = 0, is SOLUTION Concept If an equation of the form M dx N dy = 0 is inexact, it is made exact by multiplying integrating factor IF




Solve The Following X Dy Dx Y X 2 Dy Dx 2y Chegg Com



2xy Y 2 2x 2 Dy Dx 0 Y 2 When X 1 Sarthaks Econnect Largest Online Education Community
$(x^2y^2)dx−2xydy=0$ $\frac{dy}{dx}=\frac{x^2y^2}{2xy} $(i) This is a homogeneous differential equation because it has homogeneous functions of same degree 2 homogeneous functions are $(x^2y^2)$ and $2xy$, both functions have degree 2 Solution of differential equation Equation (i) can be written as,Solve the following differential equation (x2 y2)dx 2xy dy = 0Click here👆to get an answer to your question ️ The differential equation 2xy dy = x^2 y^2 1 dx determines Join / Login Question The differential equation 2 x y d y = x 2 y 2 1 d x determines A A family of circles with centre on xaxis B A family of circles with centre on y



What Is The Solution Of Math Frac Dy Dx Frac 2xy X 2 Y 2 Math Quora
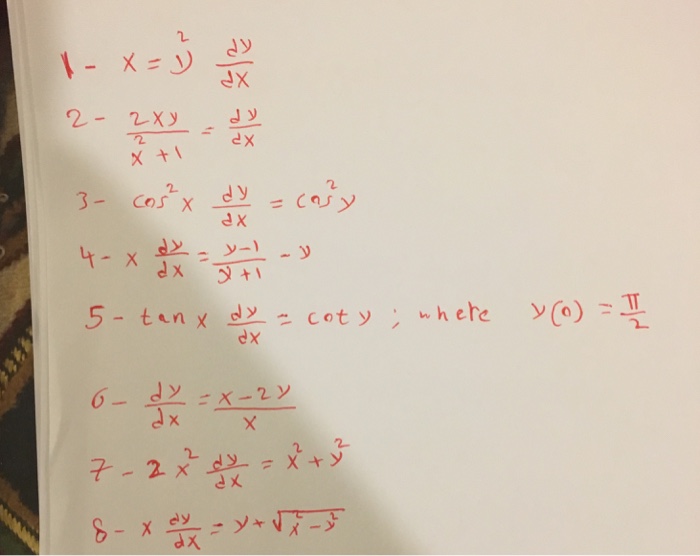



X Y 2 Dy Dx 2xy X 2 1 Dy Dx Cos 2x Dy Dx Chegg Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyVITEEE 14 The solution of (dy/dx) = (x2 y2 1/2xy), satisfying y(1) = 0 is given by (A) hyperbola (B) circle ellipse (D) parabola Check An TardigradeThis is because the coefficients of dx and dy are both homogeneous two variables functions of the same order I suggest you write the ODE as y′ = 32t2t2−t−2 = f (t), (x = 0,t = y/x) (2x^23y^27)xdx (3x^22y^28)ydy=0 (2x2 3y2 −7)xdx− (3x2 2y2 −8)ydy = 0



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora



How To Solve This Differential Problem Dy Dx X 2y 3 2x Y 3 Quora
Given the equation $$x^{2} 2 x y{\left(x \right)} \frac{d}{d x} y{\left(x \right)} y^{2}{\left(x \right)} = 0$$ Do replacement $$u{\left(x \right)} = \frac{yNotice that x 2 c y 2 = 1 c y = y 1 − x 2 So d x d y = c y − x = (y 1 − x 2 ) − x = 1 − x 2 − x y = x 2 − 1 x y How to solve the ordinary differential equation 2xy \frac{dy}{dx} = x^2 y^2 Find oneparameter families of solution curves of the following differential equations dy/dx 2xy/(1 y^2) = x^2 2 asked May 17 in Differential Equations by Yajna (299k points) differential equations;




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5



1
Hence, du/dx = dy/dx * (2y) This is the derivative of the second component4) For the third component, let w = 2xy We use the product rule dw/dx = 2x*(dy/dx * 1) 2*(y) = dy/dx (2x) 2y This is the derivative of the third component5) Overall the equation differentiates to 2 x ln(2) dy/dx(2y) = dy/dx*(2x) 2y This can be rearranged toGet an answer for 'Solve the differential quation dy/dx = (2xy^21)/(2x^2y)' and find homework help for other Math questions at eNotesClick here👆to get an answer to your question ️ Solve ( x^2 y^2 ) dy/dx = 2xy Join / Login > 12th > Maths > Differential Equations > Solving Homogeneous Differential Equation




Y 2 X 2 Dy Dx Xy Dy Dx Youtube




For Problems 26 Determine An Integrating Factor Chegg Com
Simple and best practice solution for (1y^2xy^2)dx(x^2yy2xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkDy/dx= (x²y²)/2xy Note that the function in the right side is a homogeneous function of degree 0 So substitute y=vx where, v is a function of x dy/dx=vx (dv/dx) vx (dv/dx)= (x²v²x²)/2vx² => x (dv/dx)= (1v²2v²)/2v => 2v/ (1v²) dv=dx/x => dx/x2v/ (v²1) dv=0 y = x sqrt(10/x1) We use the substitution y=vx This means that dy/dx =vx (dv)/dx Now, the given equation is 2xy (dy/dx)=y^2x^2 or dy/dx=1/2(y/xx/y) so that vx (dv)/dx =1/2(v1/v) implies x (dv)/dx =1/2(1/vv) which can be rewritten in the form 2 v/(v^21) dv=(dx)/x implies (d(v^21))/(v^21) =dx/x which readily integrates to ln(v^21) = ln x C The given initial condition is y
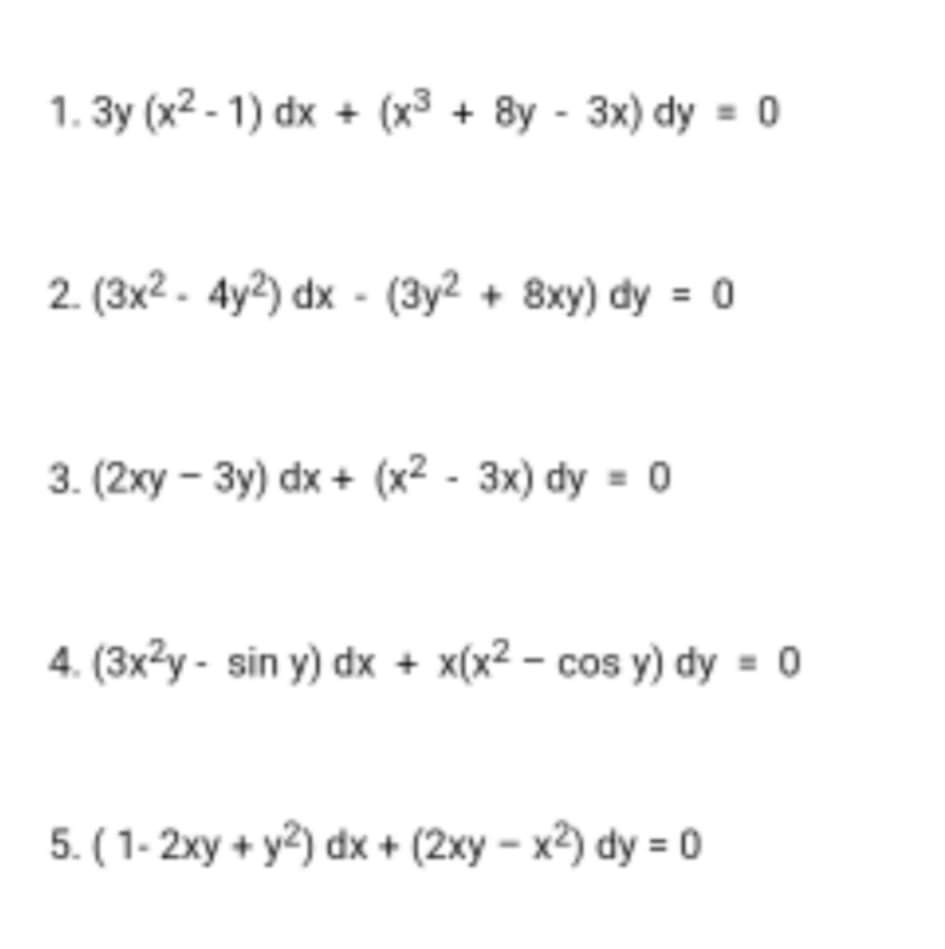



1 3y X2 1 Dx X3 8y 3x Dy 0 2 3x2 Chegg Com




1 X 2 Dy Dx 2xy X 2 2 X 2 1 Youtube
It is homogeneous equation Ex 95, 4 show that the given differential equation is homogeneous and solve each of them (𝑥^2−𝑦^2 )𝑑𝑥2𝑥𝑦 𝑑𝑦=0 Step 1 Find 𝑑𝑦/𝑑𝑥 (𝑥^2−𝑦^2 )𝑑𝑥2𝑥𝑦 𝑑𝑦=0 2xy dy = − (𝑥^2−𝑦^2 ) dx 2xy dy = (𝑦^2−𝑥^2 ) dx 𝑑𝑦/𝑑𝑥 = (𝑦^2 − 𝑥^2)/2𝑥𝑦 Step 2 Putting F(x, y) = 𝑑𝑦/𝑑𝑥 and finding FCalculus Basic Differentiation Rules Implicit Differentiation




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy




Solving The Bernoulli Differential Equation X 2 Dy Dx Y 2 Xy Youtube
Use separation of variables to solve the differential equation dy/dx 2xy^2 = 0 or equivalently written as y'2xy^2=0The steps to solving a DE by separation Ex 96, 14For each of the differential equations given in Exercises 13 to 15 , find a particular solution satisfy the given conditionThe solution of dxdy = 2xyx2 y2 1 satisfying y(1) =1 is given by The solution of d x d y = 2 x




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy




Which Of The Following Is The Solution To The Chegg Com
The solution of the differential equation dy/dx = 2xy is (a) y = ce^x^2 (b) y = 2x^2 c (c) y = ce^x^2 c asked in Ordinary asked Mar 23 in Mathematics by MukeshKumar (319k points) Let C1 be the curve obtained by the solution of differential equation 2 x y d y d x = y 2 − x 2, x > 0 Let the curve C2 be the solution of 2 x y x 2 − y 2 = d y d x If both the curves pass through (1,1), then the area enclosed by the curves C1 and C2 is equal to (1) π − 1 (2) π 2 − 1Find the particular solution of the differential equation (1 y^2)(1 log x)dx 2xy dy = 0 given that y = 0 when x = 1 asked May 13 in Differential Equations by Rachi (



How To Solve This Differential Equation Dy Dx X 2y Quora



1
The equation is M(x,y)dx N(x,y)dy =0 with M(x,y) = 2xy , N(x,y) = (x^2 y^2 1)The eq is not exact bcause M_y = 2x # N_x = 2xHowever ( N_x M_y )/M = 2/y depends only on yThe integrating factor is 1/(y^2)The equation P(x,y)dx Q(x,y)dy=0 with P = 2x/y , Q =Solve The Initialvalue Problem Dy/dx2xy=2 Y(0)=1 This problem has been solved! Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Solve The Differential Equation X 1 Dy Dx 2xy Given That Y 2 1




Exact Equations Example 3 Video Khan Academy
Calculus Find dy/dx x^2y^2=2xy x2 y2 = 2xy x 2 y 2 = 2 x y Differentiate both sides of the equation d dx (x2 y2) = d dx (2xy) d d x ( x 2 y 2) = d d x ( 2 x y) Differentiate the left side of the equation Tap for more steps Differentiate Tap for more stepsFind dy/dx 2xyy^2=1 Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of with respect to is Evaluate Tap for more steps Since is constant with respect to , the derivative of with respect to isHow do I solve (X*22xyy*2) dx (y*22xyx*2) dy=0?



How To Homogeneous Reducible Differential Equation Dy Dx 2x Y 1 X 2y 1 Quora




Solve Y 1 2xy Dx X 1 Xy Dy 0
Solve first grade ecuation with bernoulli dy/dx = (y^22xy)/x^2 general ecuation and particular when y(1)=1Dy/dx=(x^2y^21)/2xy Hi, This is a Homogeneous differential equation So put y=vx and solve, ie keeping v as avariable find dv/dx in terms of dy/dx and substiThe ODE is homogeneous ODE of order one This is because the coefficients of dx and dy are both homogeneous two variables functions of the same order I suggest you write the ODE as y′ = 32t2t2−t−2 = f (t), (x = 0,t = y/x) Find the solution of (xy^22x^2y^3)dx (x^2yx^3y^2)dy=0



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True A Solution Is X 2 Y 2 Cx B X 2 Y 2 Cx C X 2 Y 2 X C D Y 0 0
3 Q1B Solve (1) Two circles with radii 16 and 48 touch each other externally Find the distance between their centres A bouncing toy reaches a height of 64 inches at its first peak, 48 inches at its second peak, and 36 inches at its third peakSolution for (2xy)dy (x^2y^21)dx=0 equation Simplifying (2xy) * dy 1 (x 2 y 2 1) * dx = 0 Remove parenthesis around (2xy) 2xy * dy 1 (x 2 y 2 1) * dx = 0 Multiply xy * dy 2dxy 2 1 (x 2 y 2 1) * dx = 0 Reorder the terms 2dxy 2 1 (1 x 2 y 2) * dx = 0 Reorder the terms for easier multiplication 2dxy 2 1dx (1 x 2 y 2) = 0 2dxy 2 (1 * 1dx x 2 * 1dx y 2 * 1dx) = 0 Reorder the terms 2dxy 2 (1dx 1dxy 2 1dx 3) = 0 2dxy 2 (1dx 1dxy 2See the answer undefined Show transcribed image text Expert Answer 100% (1 rating) Previous question Next question Transcribed Image Text from this Question 2 Solve the initialvalue problem dy/dx2xy=2 y(0)=1




If X 2xy Y 2 2 Them At The Point 1 1 Dy Dx Chegg Com




X 2 Y 2xy Y 3 0 X 0 Dy Dx X 2 Y 3 1 Chegg Com



What Is The Solution Of This Differential Equation Y X 2 Y 2 1 Dx X X 2 Y 2 1 Dy 0 Quora



The Solution Of 1 X 2 Dy Dx 2xy 4x 2 0 Is Sarthaks Econnect Largest Online Education Community




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is Given By




The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1 X 2 1 Sqrt 1 X 2 C B Y 1 X 2 Sqrt 1 X 2 C C Y 1 X 2 3 2 Sqrt 1 X 2 C D None Of These
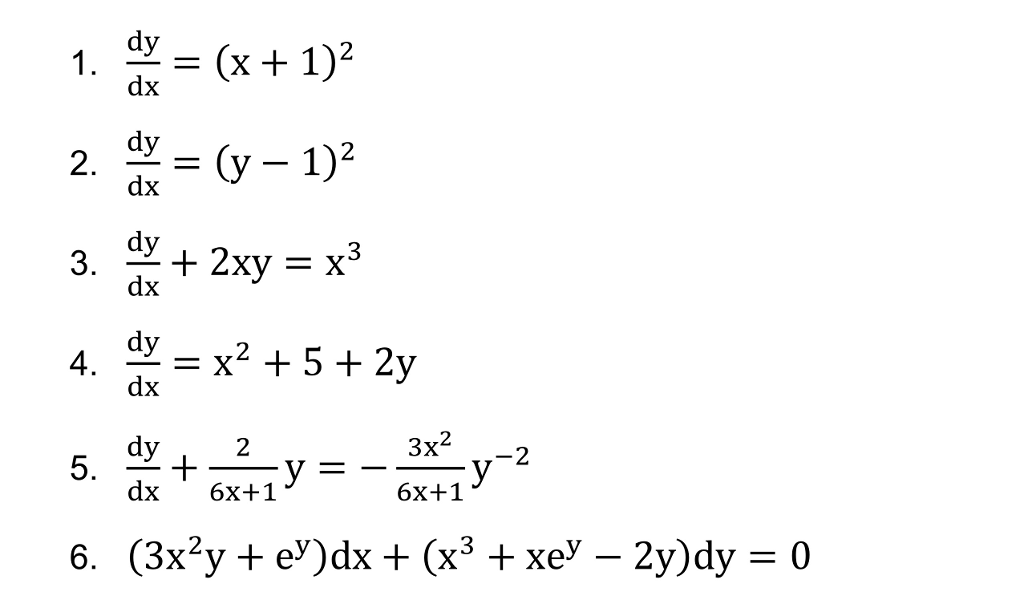



Dy Dx X 1 2 Dy Dx Y 1 2 Dy Dx 2xy Chegg Com
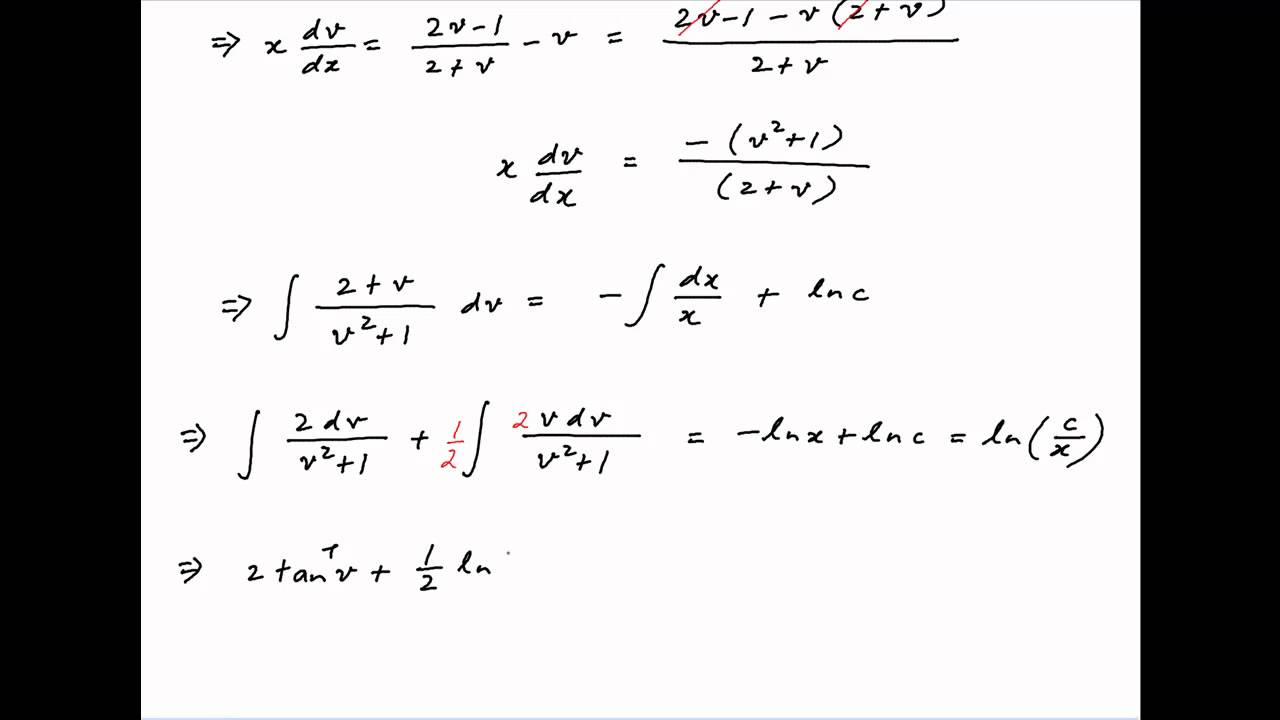



Solve The Differential Equation Dy Dx 2y X 2x Y Youtube




Engineering Mathematics Notes




Differential Equations Separation Of Variables Ppt Download




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic
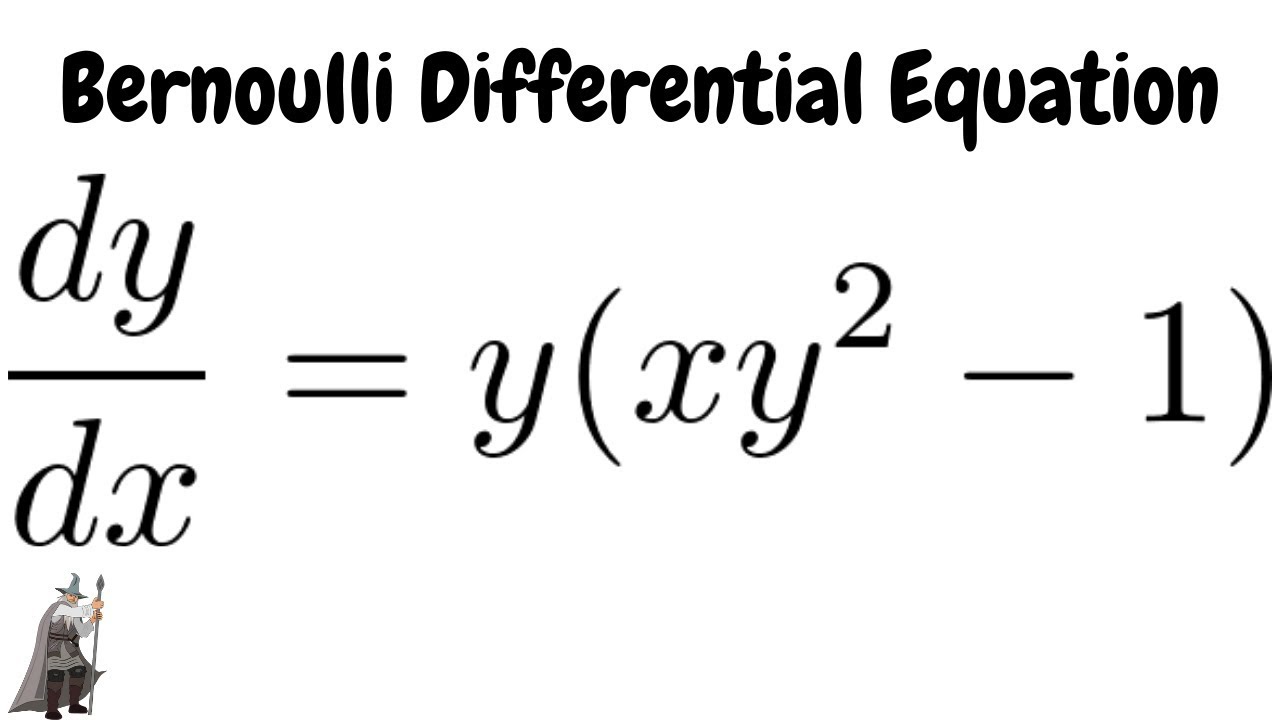



Bernoulli Differential Equation Dy Dx Y Xy 2 1 Youtube
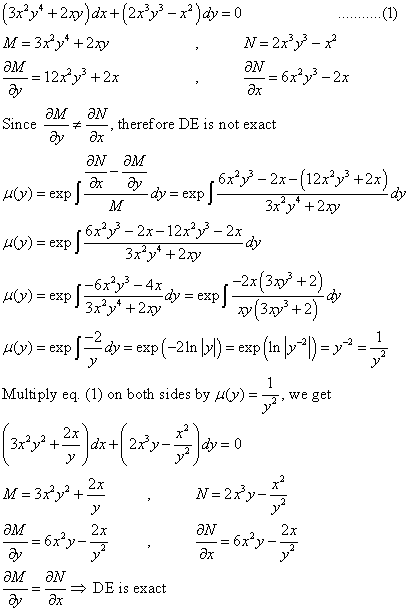



Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




Ex 9 6 8 Find General Solution 1 X2 Dy 2xy Dx Ex 9 6




In Solve The Given Initial Value Problem X Y 2 Chegg Com




Solve Dy Dx 2xy X2 Y2 The Answer Given In The Book Is Y C X2 Y2 Brainly In



Solve The Following Differential Equation X 2 Y 2 Dx 2xy Dy 0 Given That Y 1 When X 1 Sarthaks Econnect Largest Online Education Community




Use Implicit Differentiation To Find Dy Dx Xy 4 Chegg Com



How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora




Example 9 Find General Solution Of Dy Dx X 1 2 Y Examples




Find The Explicit Particular Solution Of The Initial Chegg Com




9 Solve Dy Dx 2xy X 2 Y 2 10 Solve 2xydx 1 Chegg Com



How Do L Solve The Initial Value Problem X 2 Y 2 Dy Dx Xy Y 1 2 Quora



Solve The Differential Equation X 2 1 Dy Dx 2xy 1 X 2 1 Sarthaks Econnect Largest Online Education Community



X 2 Y 2xy Y 3 0 X 0 Dy Dx X 2 Y 3 1 Chegg Com




Determine If The Given Ode Is Exact Or Not If It Is Chegg Com




X2 1 Dy Dx 2xy X4 2x2 1 Cos X Solve This Differential Maths Differential Equations Meritnation Com




1 Given The Differential Equation X2 2xy Y2 Dx Y Chegg Com
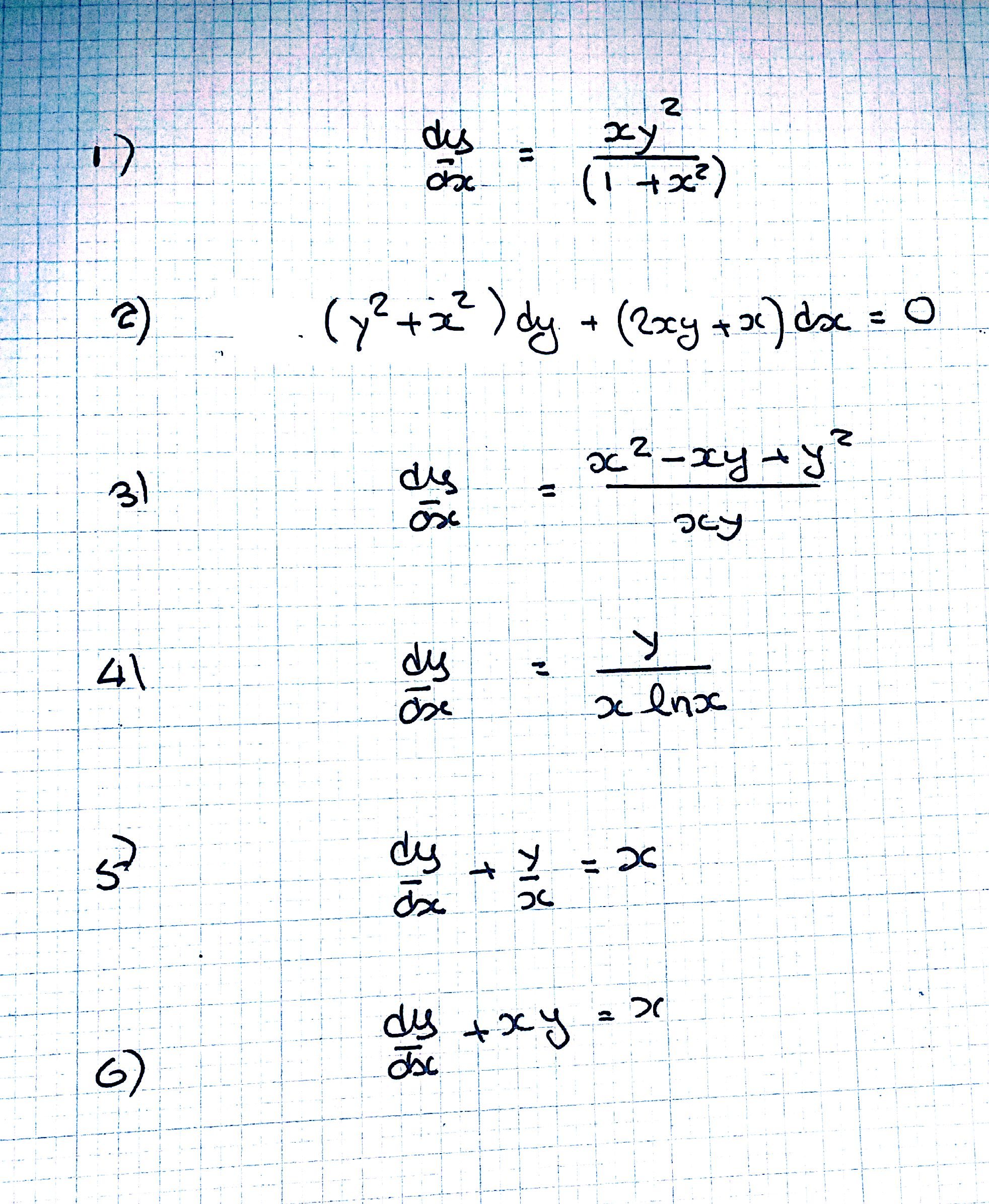



Dy Dx Xy 2 1 X 2 2 Y 2 X 2 Dy 2xy Chegg Com




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube




Solve Dy Dx X 2 3y 2 2xy Youtube
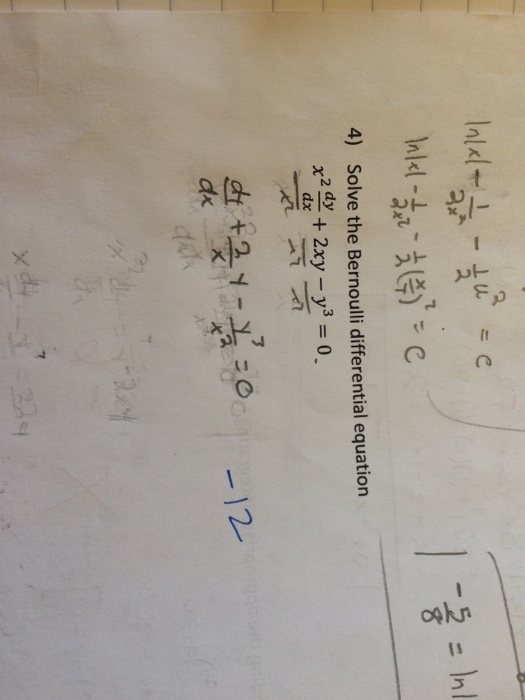



Solve The Bernoulli Differential Equation X 2 Dy Dx Chegg Com
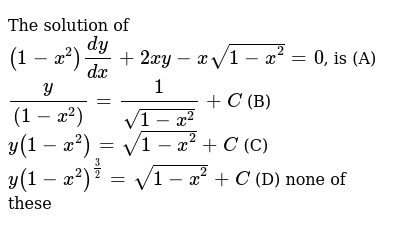



The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1 X 2 1 Sqrt 1 X 2 C B Y 1 X 2 Sqrt 1 X 2 C C Y 1 X 2 3 2 Sqrt 1 X 2 C D None Of These




Calculate The Iterated Integral Integral 0 3 Chegg Com
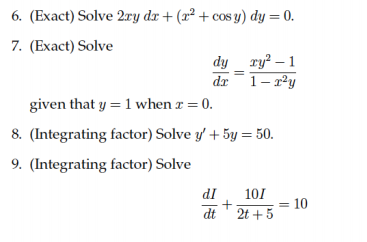



Solve 2xy Dx X 2 Cos Y Dy 0 Solve Dy Dx Chegg Com




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Use Implicit Differentiation To Find Dy Dx Xy X Chegg Com




Solve Dy Dx 1 X Y Solve Dy Dx Y X 1 Y Solve The Chegg Com




Solve The Following Initial Value Problems 12xy 2 Chegg Com




Solve The Given Differentia By Separation Of Chegg Com




Which Of The Following Is The Solution To The Chegg Com
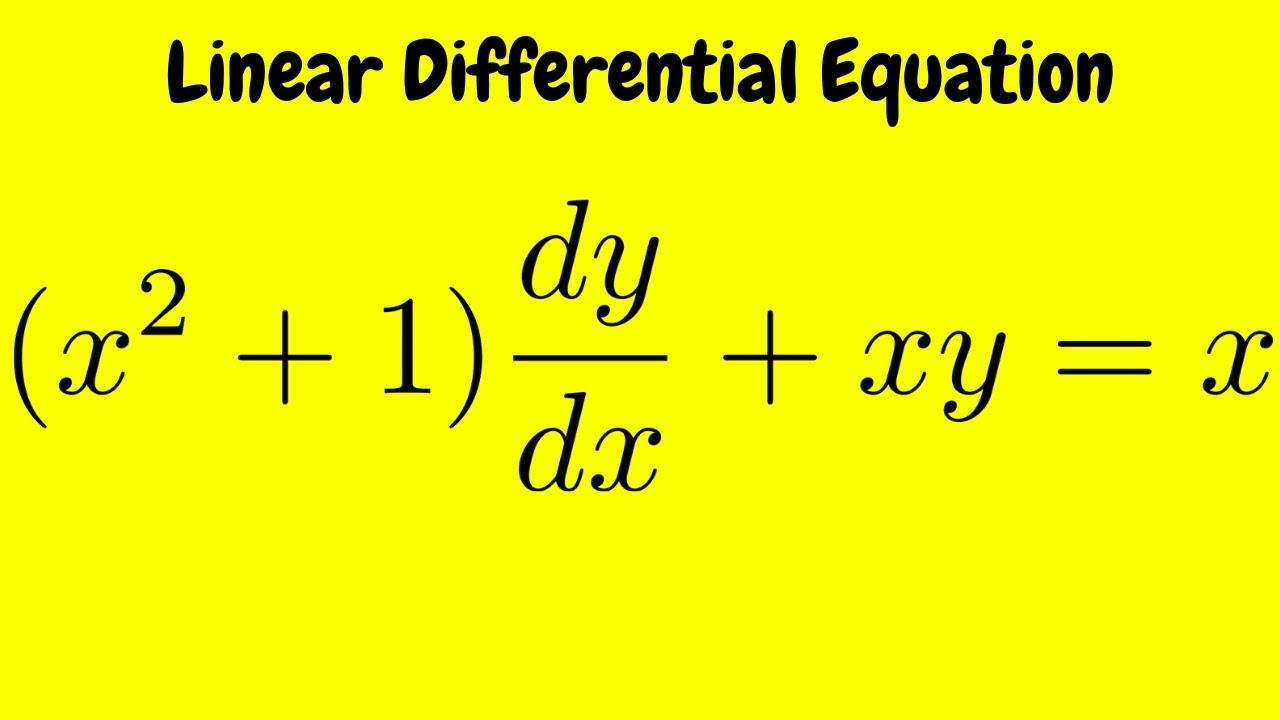



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora



The Solution Of Dy Dx X 2 Y 2 X 2 Y 2 1 2xy Satisfying Y 1 1 Is Given By Sarthaks Econnect Largest Online Education Community




2xy Dy Dx X 2 3y 2 Youtube




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is Given By



Solve The Differential Equations 1 X 2 Dy Dx 2xy X 1 X 2 Sarthaks Econnect Largest Online Education Community
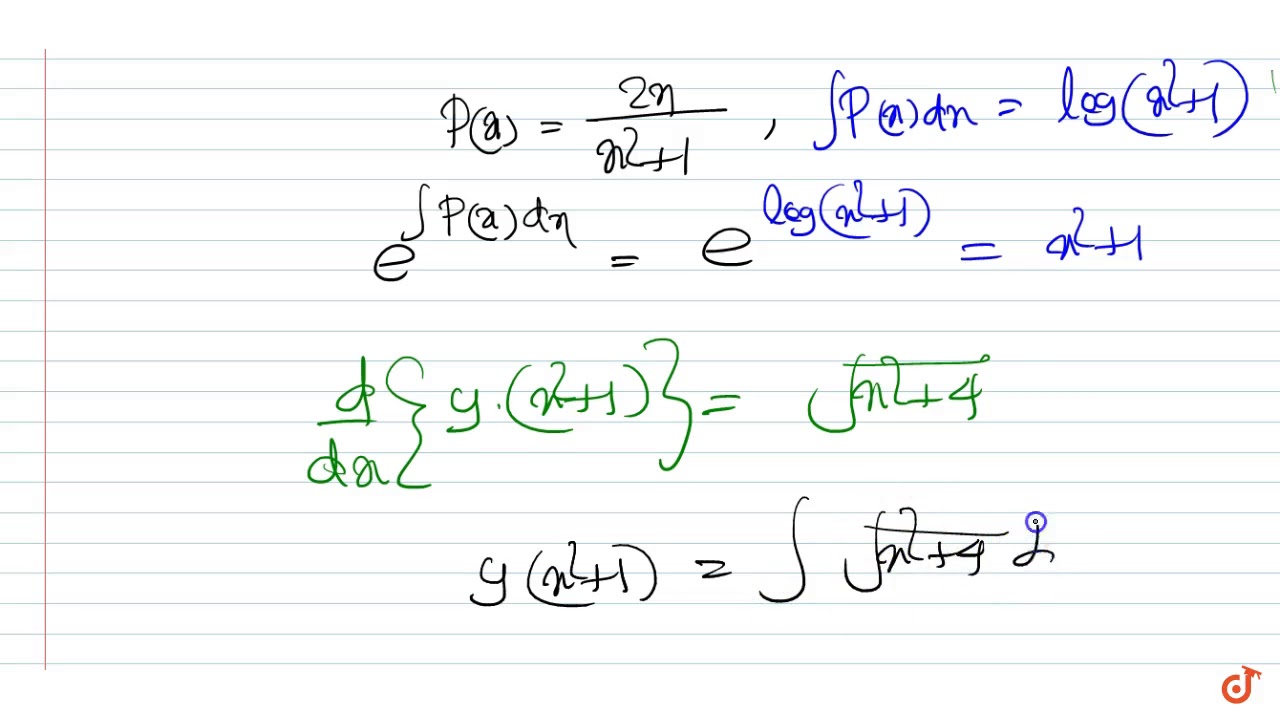



Solve X 2 1 Dy Dx 2xy Sqrt X 2 4 Youtube



What Is The Differential Equation Of Dy Dx X 2 1 Y 2 1 Quora



Solve The Following Differential Equation 1 X 2 Dy Dx 2xy 1 1 X 2 Given Y 0 When X 1 Sarthaks Econnect Largest Online Education Community



Solve The Differential Equation Dy Dx 1 X Y2 Xy2 When Y 0 X 0 Studyrankersonline



Www Tau Ac Il Levant Ode Solution 6 Pdf




X 2 Y 2 Dx 2xy Dy 0 Youtube




Solve The 1 St Ode Dy Dx X 2 3y 2 2xy X 0 Chegg Com



Solved Test Exactness And Solve Question 1 2xy 3x 2 Dx X 2 2y Dy 0 Question 2 Cosx Xsinx Y 2 Dx 2xydy 0 Question 3 2xydx X 2 Course Hero




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube




How Does 2xydx Y 2 X 2 Dy 0 Quora
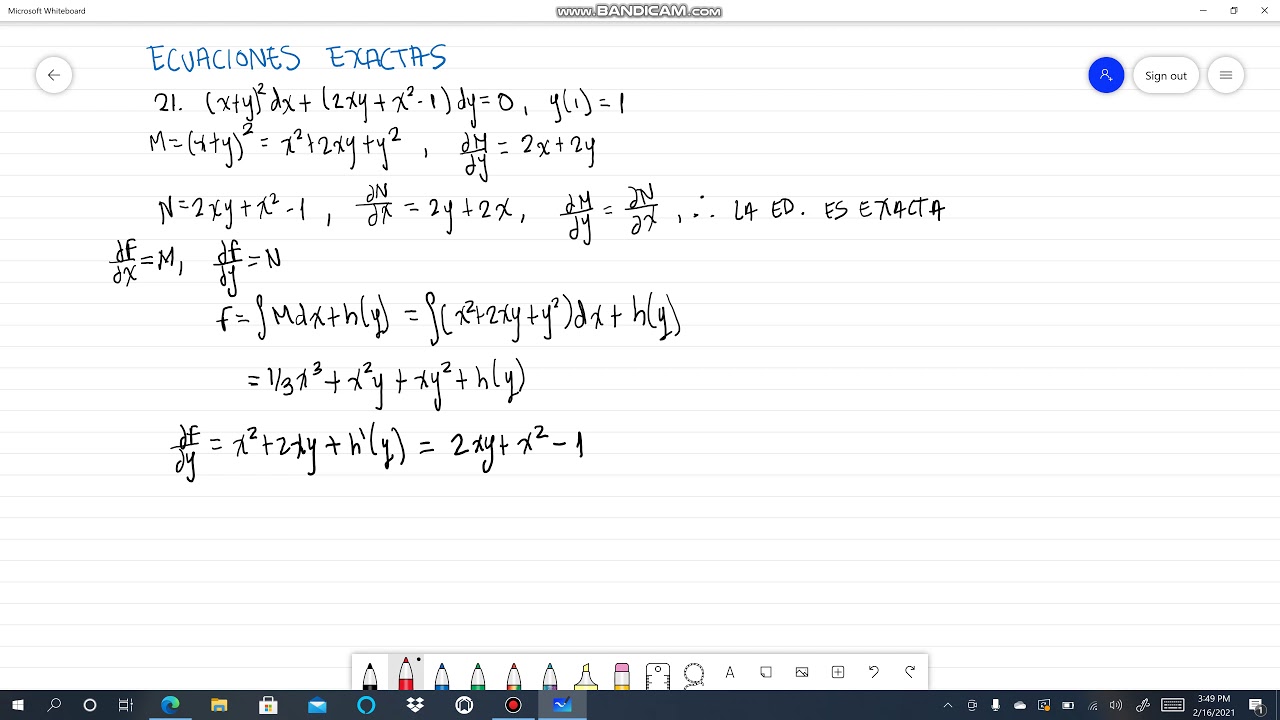



21 X Y 2 Dx 2xy X 2 1 Dy 0 Y 1 1 Ecuaciones Exactas Alexander Estrada Youtube



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation



Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline




Answered In Exercises 1 1 Evaluate The Bartleby
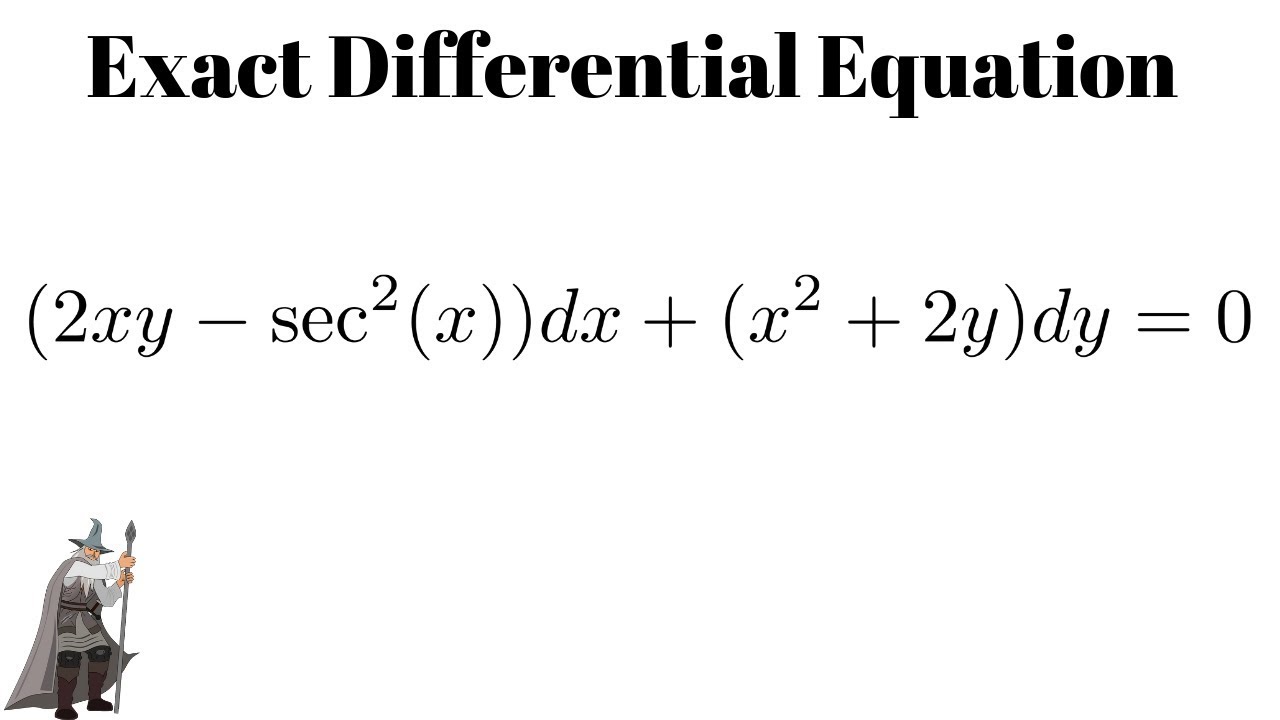



Exact Differential Equation 2xy Sec 2 X Dx X 2 2y Dy 0 Youtube
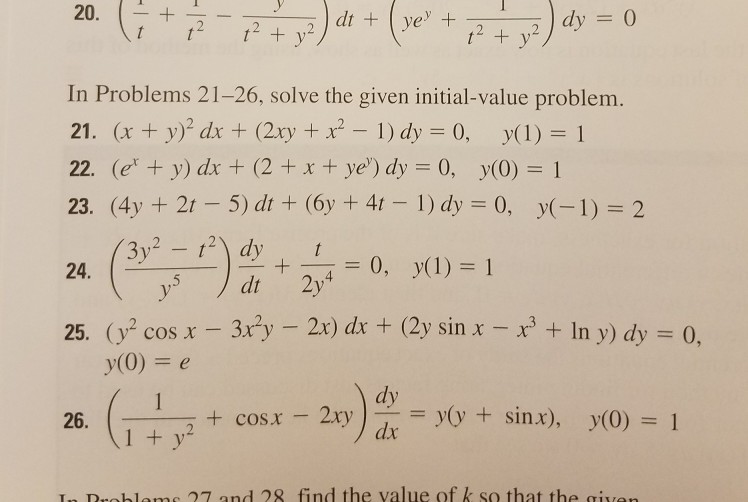



In Problems 21 26 Solve The Given Initial Value Chegg Com



Bernoulli Differential Equation X Dy Dx Y 1 Y 2 Youtube




If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is Given By




15 The Differential Equation 2xy Dy X2 Y2 1 Dx Determines A A Family Of Circles With Centre On X Axis B A Family Of Circles With Centre On Y Axis



1




Solve Dy Dx 2xy Y2 X2 Maths Differential Equations Meritnation Com




Find An Explicit Solution Of The Initial Value Chegg Com




4 Solve The Exact Differential Equation 1 2xy Dx 4y3 X2 Dy 0 4 Solve The Exact Differential Equation Homeworklib




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is Given By



Solve X 2dy Dx 2xy Y 2 Youtube




X 2 Y 2 Dx 2xy Dy 0 The Solution To This Differential Equation Represents Which Curve



0 件のコメント:
コメントを投稿